最近在iPad的iTunes U上看了這場演講。 我覺得很精采！ 所以想在此分享給各位。

演講者名叫Andrew Lo，是一個Finance的教授、也是MIT Sloan School的Management Director。 他演講的主題是Physics Envy(物理忌妒)。

可能得要先說明一下，到底「物理忌妒」是啥。

所謂「物理忌妒」，指的是在很多專業領域中，大家認為其中的理論最終應該要像物理學一樣，能透過數學模型的方式加以解釋或呈現。 最完美的，希望要像牛頓定律那種，靠簡單的數字與模型來「標準化某些反應」。

這是過去很多專業學術上迷失的一個方向。 因為某些層面的知識，如財務、經濟、專案、哲學、心理學等，並不像物理學一樣可以透過數學來加以解釋。 他們通常都涉及到人性，也涉及個人偏好的心理反應。 這些東西不一定適合被數據化，事實上往往根本也無法被數據化。 比方以財務或經濟學來看，一些學者試圖構築經濟或財務模型，透過分析來計算如「GDP」、「合理股價」、「經濟指數」、「CAPM」之類的東西，就是物理忌妒的結果。

這類分析通常都有一個偏誤的前提假設 - 也就是「人的純粹理性」，並以這前提來計算甚麼是「正確的」。 但因實際上人的理性假設並不成立，所以也造成模型往往遠偏離現實。 把「不理性的層面」排除雖然讓結構看起來簡潔又漂亮，但卻毫無實用意義。

專案管理有時候也有類似傾向。 大家常以為一定要把狀態化成數字或是燈號才叫好的管理。 可是很多人常常沒意識到，數字或燈號未必就是所謂的「真實」，通常也只不過是一個相對的參考，使用起來得很小心。 所以呢，是否一定需要數字或是燈號，其實得看狀況而判斷，而不能照本宣科的認為數字就一定可以完美呈現真實狀況。 有時適度模糊，或是靠平衡的政策與組織權限一樣能達到好的結果。 換言之質化與量化的平衡，是管理者不能偏廢的功夫。

對物理忌妒這議題有興趣的讀者可以參考這一篇 http://en.wikipedia.org/wiki/Physics_envy

不過，我分享這篇演講的原因在於他很傳神地解釋了「風險」(Risk)與「不確定性」(Uncertainty)的差異。 而這剛好是很多人常有的疑問(像過往上課時，就很多人會問我這兩個字的差異)。 所以貼出這篇，我覺得應該對很多人是會很有啟發性。

Risk，指的是可以預先知曉，但無法完全掌握的事件。 但Uncertainty，則是完全不可預估的事件，也就是專案管理書籍裏頭會提到的Unknown Unknown。 像Andrew就提到：「某些物理現象因為變動已被人熟知，所以可以用數學方式定義；但其他社會科學的東西，則因為很多變動變因太大，你無法取得所有參數，數學是完全無法解釋的」。

他也另外提到：「在現實上賺錢的多寡，其實跟承擔風險無關；而是跟承擔不確定性有關」。 像他又舉例，人壽業就是個目前大家掌握度很高的產業。 只要提供一個人的生活習慣、飲食習慣、家族遺傳、抽菸喝酒的傾向，能活多久其實可透過數學公式與參數來預估的。 雖然也偶有例外，但大部分的準確度其實還滿高的。 也由於掌握度已高，就造成產業獲利空間被壓縮。 但反過來說，若是一個極度創新的事業，因為面對太多unknown；尤其那些走出過往不存在business model的產業，也就充滿無限機會，市場也會給予更高的報酬。

但怎麼了解自己面對的是甚麼呢？ 他提到他建議把Uncertainty延伸成五個Level：

Level 1: Complete Certainty (完全確立)
Level 2: Risk without Uncertainty (已知道機率分布曲線)
Level 3: Fully Reducible Uncertainty (假如收集資料，可以建構分布曲線)
Level 4: Partially Reducible Uncertainty (可觀測，但觀測時又變動的事件。)
Level 5: Irreducible Uncertainty (完全無法掌握的狀態)
(詳細的說明可參考演講的影片，他特別有用物理案例來解釋這五個等級)

他並建議大家在面對情境時，要自我分析處在哪個Level，並找出對應的處理方式。 低度不確定性時，數學是個好幫手。 比方說，如果你在Level3之前，多收集數據有可能逐步了解整個狀態的機率分布，並轉化成可被推估的分析表。 像他前例提到的人壽產業，就是一個接近成功的案例。

但在高度不確定性時，你就不用費心想提高預測度，其他層面的策略反而變得重要。 像總體經濟學，很多人就是一直在試圖用數學來解決Level4的問題，也因此才困在目前的局面中。 數學模型看似完美的狀況，卻每每被人性的影響所偏移。 他甚至開玩笑提到，像最不確定性的學說就是宗教，而就明顯是數學無能為力的領域。

他有句話我這裡想Highlight一下：當面對不同程度的不確定性時，不該用不對的方法來對應。 但又怎麼知道哪個狀況該採取甚麼策略呢？ 他提供了一個不確定性檢查表(Uncertainty Checklist)。

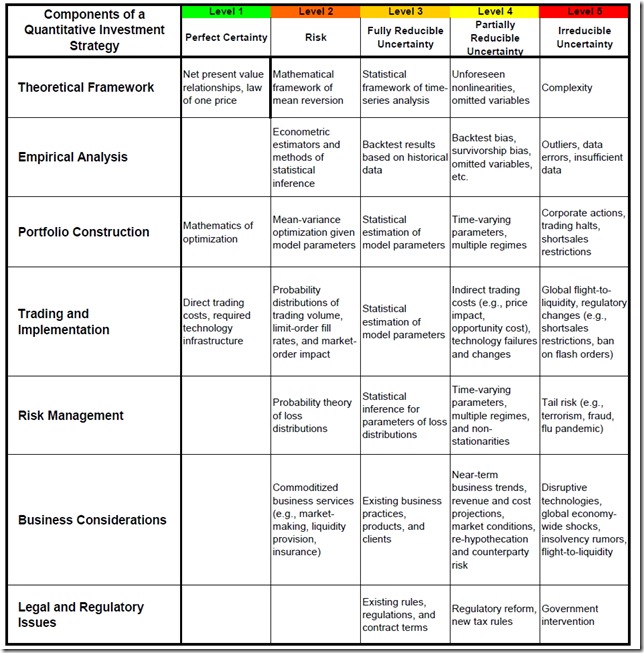
(上圖) 不確定性檢查表。 這張圖是我從他論文中擷取貼上的。

我之所以想分享這篇。 主要在於很多時候，人們確實在問題解決上有所盲點。 我自己體驗很深的有兩個領域 - 一個是金融投資，一個是專案管理。 這兩個領域其實都已經不是Level 1到3的狀況，但很多人卻總試圖想透過「提高預估能力」這條路來解決問題。 以金融投資上來講，很多人就試著想做股價分析、本益比分析、公司價值計算、技術分析、或是波浪理論這類東西想找出一個規律，並以此提高預測率。 但實際上通常都會發現一切是徒勞無功。 專案管理也是類似，很多人希望訓練員工更正確的預估工期，認為這是讓專案掌握度更高的關鍵。 甚至某些公司還會刻意處罰預估與實際的落差。

但實際上這些其實是不太對的。 當Randomness過高時，你在工作或執行層級想提高預估率，其實幫助很低，還不如採取一些High Level的策略調整。 比方說，股價無法預估，那你恐怕該從加碼策略、停損策略、或是資金運用策略上去思考。 以專案管理來說，天期預估不準，但是否該改以獎勵策略上鼓勵盡量提早完工這類行為？ 這樣其實才能把事半功倍，而非事倍功半。

如果你能從更High Level的角度思考問題，不確定性的擾動其實有時候可以跨過不計(Andrew也有舉個例子，詳情可以看演講的Video或是看我後面附錄的翻譯)。 當然，這樣的解法或許不夠優美、也沒有非常的精確與科學。 但問題解決，永遠才是最重要的呢。 千萬不要讓物理忌妒，干擾了你我的決策能力。

延伸閱讀

他的論文: http://web.mit.edu/alo/www/Papers/physics8.pdf

他的演講: http://mitworld.mit.edu/video/794

附錄

為了服務英文不很好的讀者，我大致講一下他在演講中提到Risk VS Uncertainty的一個心理問題(與推導)。

他說，有個箱子，裏頭放了紅色與黑色的球，其中紅色與黑色各半。 如果抽出來的球跟你選的顏色一樣，你可以贏得USD$10,000，但只能賭一次。 然後問大家，你想選哪個顏色？ 並且願意投入的賭金上限是多少？

大家舉手，發現「民意」上限最高落在$4,500-5,000之間。 他解釋說，這很合理，因為大家都會計算期望值(Expected Value)。 很多人甚至願意出價遠低於$4,500，這是因為要冒險總是要有高於期望值的回報嘛。

(附註，在這賭局中，可知機率分布。 所以是個純Risk的問題)

再來，他說又有另一場賭局。 這次賭局的規則不一樣。 事先你不知道顏色分布，莊家可以按照他的喜好自訂顏色分布。 其他規則都相同。 一樣問大家想選甚麼顏色？ 以及願意投入的賭金上限是多少？

這部分就開始非常有意思了。

他先問大家想選甚麼顏色。 有人選擇紅色。 他就問對方：「為何選擇紅色呢？ 是因為你偏好紅色，還是因為你猜我偏好紅色？ 」觀眾哄堂大笑。 但這確實，因為你不知道盒子裏頭的分布，所以你選甚麼顏色就開始有差異了。 而差異則從機率問題轉變成心理問題。

(附註，在這賭局中。 你不知道機率分布，這也就是Uncertainty了)

再來他又請大家舉手投票願意投注多少錢。 這次願意出高價的人變很少，只有一個人維持跟前一次相同的出價。

但他馬上解釋。 雖然你不知道分布是多少，但其實就機率而言，兩種顏色出現的機率還是 50：50，所以兩次賭局的實際狀態是一樣的。 人在投注上面，也應該反應相同的決策才是。 可是呢，他的經驗顯示。 就算他跟別人說這兩賭局的機率一樣。 一般人還是不願意在第二賭局上多投注。

接下來就有人舉手反應：「雖然數字看似如此，可是大家會考慮心理性的議題。」 「因為實際的分布不是隨機的，是莊家選的。 加上這遊戲又只能玩一次，如果對方能猜測我的偏好 (如我喜歡紅色)，他可能放出全黑的分布。 那我不就輸了？ 所以期望值並沒有參考價值。」

Andrew則回應到：「這其實對雙方而言都是猜測。 因為我會猜你，但你其實也會猜我。 我(莊家)猜你會了解我的偏好而做的選擇，也可能剛好掉入你設的陷阱。

他就問到。 在這狀態下，如果你真被逼著非要參與這樣一個賭局。 可是你又不希望你因為情緒影響而被莊家猜中你的心思，而讓他放出一個不利於你的顏色分布時，你能採取甚麼策略？

他的答案很有趣。

他說：「可以採取亂數策略」。 用亂數來擾亂亂數。 你若丟銅板來決定顏色，那莊家就一定猜不到。 這時候，莊家最安全的方法其實就是放50紅色與50黑色。

結果反而對你與他都公平也安全了。

你看。 要讓這高度Uncertainty賭局的結果變成可以預測的方式，其實不是強化猜測莊家心思的手法，而是跳脫從另一個層面來思考。 採取亂數的擾亂策略後，你逼著讓整個情境變化，最後反而排除了Uncertainty並變成純粹Risk的問題。 這也就是我文章結論想凸顯的重點！

很有意思，也建議大家花時間思考一下。