前兩週去工研院上Oracle Risk Analysis的操作應用課程，所以手邊在準備相關的素材。 邊準備就邊想到，蒙地卡羅風險分析是一個很多人聽過讀過，可是常搞不清楚是做什麼的玩意。

最起碼我自己每次講到PMBOK風險章節時，同學都會針對風險定量分析(Risk Quantitative Analysis)問很多問題。 所以就想到可以寫這麼一篇文章，來跟大家談談所謂蒙地卡羅風險分析法到底是在做甚麼。

不過，在一開頭，要先幫大家破除一個謬思。 因為很多人總以為這類風險分析軟體是能「自動」幫忙分析專案風險。

可惜，這是不可能的。

電腦是比人笨很多的東西。 它可以幫我們大量運算，可是前提是要有「人」把相關參數告訴電腦。 所以蒙地卡羅風險分析軟體，是無法「主動」幫我們判斷風險。 可是，如果電腦不能主動判斷風險，那它到底能做甚麼事情呢？

為避免講專案的例子太抽象，我試著舉個比較生活化的例子。 做專案蒙地卡羅風險分析，就好比拿運動遊戲來作球隊勝率的模擬分析一樣。

甚麼意思呢？ 市面上有很多運動經營模擬遊戲，棒球、籃球、足球都有。 我手邊一下有比較多資料的是足球遊戲，所以就以這當例子好了。

這類遊戲通常都有現實球員的詳細資料，其中會根據統計資料把球員能力轉換成某種數值化的差異。 守備率、射門率、速度、控球、控球、盤球力、傳球、頭鎚、開角球、開自由球、反應等等不同能力的統計資料（或定性數值）。 更完美的還會模擬場上的狀況，如天候、手球、犯規、不同部位受傷、體力耗損等。

你要經營一個球隊，一個球員是不夠的，你需要正式上場的球員、也需要候補球員，還需要考量不同的隊形與戰術。 不同戰術又須考量不同球員的適性與數值，也需要找不同屬性的球員。 有人適合長射、有人適合短傳、有人強於防守、有人適合4-4-2的陣勢、有人適合3-5-2的陣勢等等。

而也因為是模擬實際職業比賽，所以球員都有身價。 廣泛能力強的，通常簽約金很高；有明顯缺點的，簽約金可能就比較便宜。 所以這類遊戲的樂趣，一方面在於經營球隊，另一方面也在於有沒有可能組合出一個「能夠互補卻不花太多錢的球隊」。

當然，遊戲是否模擬周延的問題我們暫且先放一邊。 假設遊戲能把環境模擬得非常充分，一個球隊的教練甚至可以以此來測試球員組合並用來做為實際球隊建置的考量。

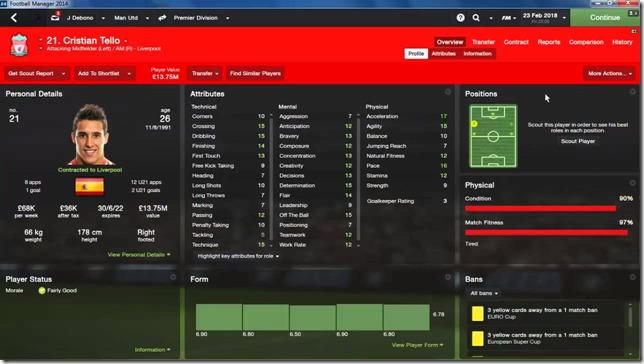
首先，他可以考慮覺得合適的球員。 決定簽約金，並把人招募進來。

(上圖，了解球員以及相關的統計能力數值)

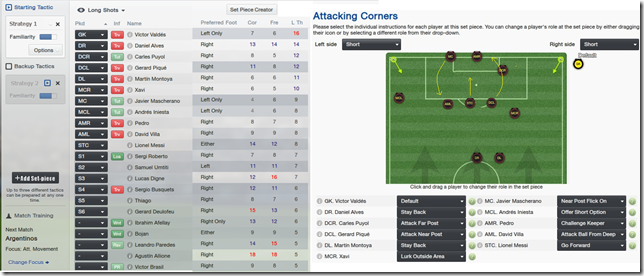
再來，根據招募來的球員，決定合宜的戰術、隊形、以及位置排列。

(上圖，設定球隊的戰術與球員位置調度)

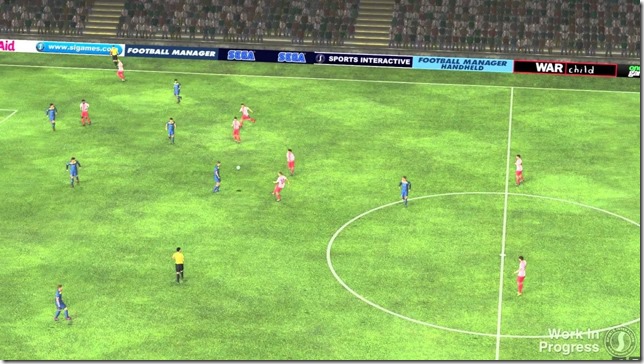
最後，就可以跟同一聯盟的其他球隊來模擬比賽。

（上圖，比賽模擬）

也因為數值都是模擬化與統計化的結果，只比一場當然沒有任何實質意義，所以通常你該試著比個100場甚至1000場。（有些軟體可以不跑3D動畫，很快速的模擬後以報表呈現數據） 然後分析自己這樣的球隊在這樣的比賽場數中，能獲得多少比例的勝率。 若1000場比下來，我目前組合的勝率不高，那能不能微調隊形、戰術、甚至把A球員賣掉換另一個人進來。 然後重新比個1000場，看看勝率有顯著的變化。

這樣模擬下來或許會發現，原本以為最重要的明星球員佔了很高的預算，但若換個平均能力值少一半的便宜球員，對勝率影響其實微乎其微，而省下的預算可以用在別的地方。 這時候就能以更合理的金額組一個效率最大的球隊。

好，以上的描述基本上現實中恐怕還沒辦法完全實現，因為尚不存在能這麼完美模擬球場狀況的模擬器。 不過就理論而言，只要能把球員的能力根據統計資料完整累計，並把球場上的各類因素都考量進來，球員對於比賽勝率的影響是可以透過多次的模擬比賽而有所參考意義。

這概念你若能看懂，那專案上面的蒙地卡羅風險分析也就是在做一樣的事情了：讓一個規劃好的專案重複執行一定次數，並看看在考量各類不確定性後，專案最可能的完成時間、資源需求、以及總成本會是如何？ 原訂完成時間多高的機率可以完成？ 以及若投資風險的降低事宜（回應計畫），到底是否值得？

那具體作法會是類似這樣：

首先，你先把專案的WBS拆解好，WBS下各工作包的工作清單、工作邏輯、工作工期都規劃好，你會得出一個專案的基本排程。 這時候，這個計劃就可以倒入Risk Analysis程式中(或是在軟體中自己建立排程規劃也行)。

再來，你可能會在這份專案計畫中加入各類的不確定性。

比方說

1 工作本身的不確定性。

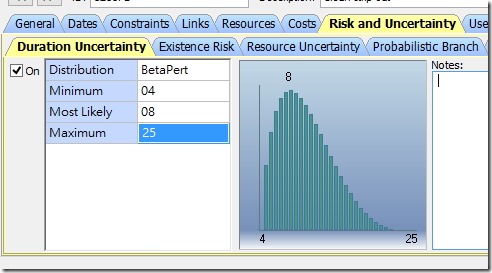
舉例而言，一項工作可能按照Beta的機率分佈，工期從3天到15天之間。

2 工作是否存在的不確定性。

什麼是工作是否存在呢？ 舉例來說，基礎開挖可能有一定比例會挖到地下水，這樣就得花時間抽水，也就會多一個抽水的工作。 在這案例中，就可以透過Task Existence的功能來模擬 - 一定機率是只有開挖，但另有一定機率會多增加一個抽水的工作。

3. 工作路徑分歧的不確定性。

什麼是路徑分歧呢？ 舉例來說，材料進料後有一定比例的機率可能要驗退並重新等待，有一定比例的機率則可以直接進入Prototyping。 所以可以把兩條路徑都建立起來，給予分別的機率，然後模擬不同路徑分歧對專案的影響。 萬一我們選擇便宜的供應商導致，材料問題增加，對要徑是否會產生任何變化？

4. 邏輯上的不確定性。

所謂邏輯上的不確定性，指的是作業的前置任務有可能因為另一件事情發生而取消。 比方說某個設備我們想找當地的代理商購買。 可是若代理商沒貨，我們則可能跟國外詢問。 那這兩種可能性都可以排進計畫，可是每次專案執行只會有一種狀況發生。 要就是代理商有貨，我們跟他進貨；不然就是代理商沒貨，我們找海外。 所以船運的前面有可能是連結到任何一路線。 而這就是邏輯連結上的不確定性。

5. 資源的不確定性。

這應該很容易理解。 工程師在某一工作的投入可能介於50-70小時之間；特定溶劑在某一工作所需要的量可能介於10kg-12kg之間。

6. 風險造成的不確定性

那最大的重頭戲，自然就是專案的風險清單了。 PMBOK中界定了六個流程。 從Plan Risk Management、Identify Risks、Perform Qualitative Risk Analysis、Perform Quantitative Risk Analysis、Plan Risk Responses、到Control Risks。 認真要做風險管理的，也可以把這整套流程需求都在工具中展現。

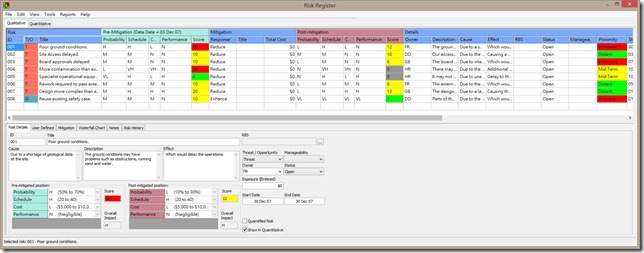
比方說，專案的風險清單：

（風險清單，涵蓋風險描述與RBS與處理前後的風險評分。 上圖，點選可放大）

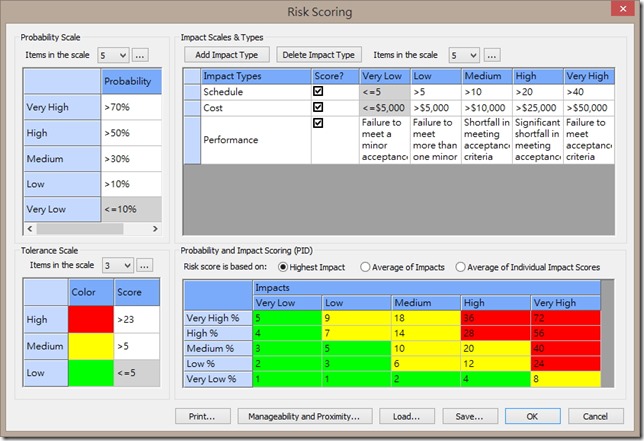
風險評分定義與風險矩陣：

（上圖，點選可放大）

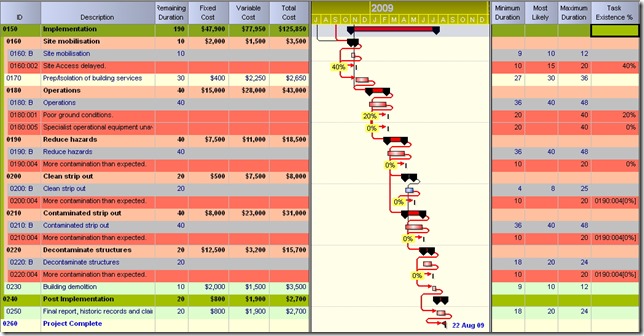
風險與工作的連結：

（上圖紅色的部份都是風險清單的內容。 透過工具我們把風險清單跟工作清單整合在一起。 這樣在做風險排程時，這些風險若被亂數觸發時，則會拉長或縮短相關工作的工期。）

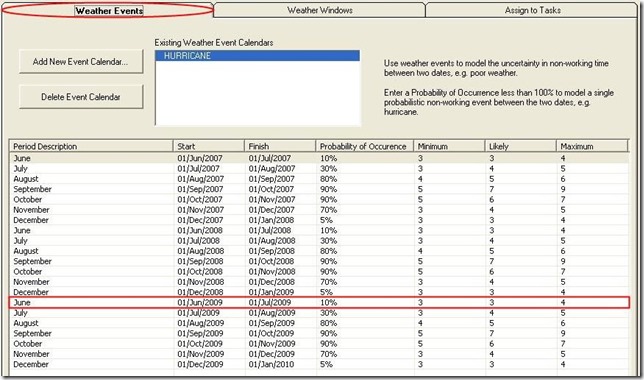
7. 天候模擬

模擬天候對專案可能造成的影響。 以台灣而言，颱風可能會造成工地現場無法施工。 美加日本最近的大雪，則是另一個例子。 所以這類天候造成的專案停工，則可以以此來模擬。

(上圖，天候模擬。 點選可放大）

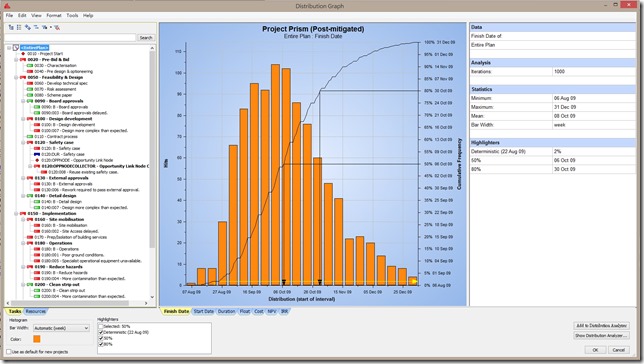
最後，當這些「不確定性」（無論是工期本身的不確定性，或是源自於風險的不確定性）都設定完成後，即可以開始讓電腦根據這樣的專案規劃默默的去執行幾千或幾萬次。 然後告訴我們按照這樣的機率分佈，到底專案最有可能在何時完成？ 花多少錢？ 總工期會是多少？ 哪些工作最可能變成要徑？ 原來設想的完工日到底有多少％的信心程度？

（上圖，這案子把不確定性都考慮進去後，最可能的完成時間是09年10月06日之後。 原來設定的完成日（黃線）則不到5％的完成機率。 備註：上圖點選可以放大。）

回應計畫的成效比對

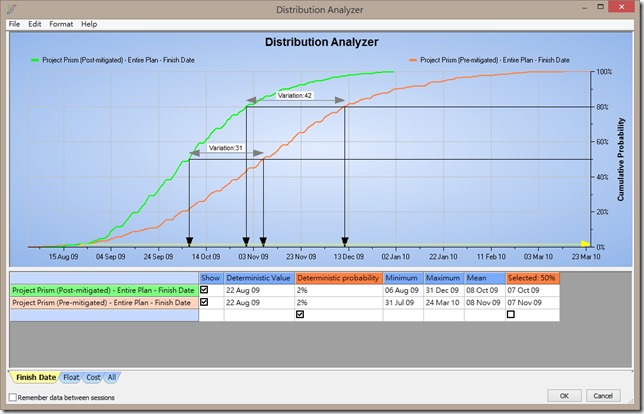
此外，我們對於風險可能會做回應計畫（還記得 Acceptance、Mitigation、Transfer、Avoidance這些手法嗎？）。 所以我們也得分析，風險回應計畫的效果如何。 舉例而言，我們投入了＄50萬買額外的設備，這樣的設備是否有效的縮短工期、還是其實沒變？ 如果沒變，我們這50萬是否應該分散到其他的風險回應計畫中？ 所以反覆實驗後，我們會更清楚風險預算該如何分配。

（上圖，風險回應計畫前後的比較。 橘色圖是風險回應計畫前的完成日狀況，綠色則是風險回應計畫後。 所以我們可以比較某項投資到底對於不確定性的收斂程度有起怎麼樣的作用。 點圖可放大）

所以，蒙地卡羅風險分析就如同透過統計與模擬比賽來組運動隊一樣。 電腦沒辦法「自動」辨識專案哪裡有風險。 可是若你提供清楚的統計數據，電腦則可以靠大量的模擬，告訴你這些不確定性的影響可能在哪裡，最可能的完成時間大約在何時，並分析回應計畫到底是否值得，又是否應該把這預算移去他用。

希望這樣的一篇文章，能幫助大家更了解這樣的分析手法。 ：）

 

沒營養的後記：雖然最上面的運動遊戲圖片是取自於SEGA的Football Manager，但我為了寫這篇想了解這類運動模擬遊戲，還真的去買了一套EA的FIFA Manager 14來試玩呢。 光為這點，大家就該好好讚一下了吧？ :P

封面圖片來源：http://3.bp.blogspot.com/-N9GApXtfwe4/UlCqKkfBW0I/AAAAAAAAC28/1bo-deu8BvU/s1600/dice1.jpg

本站所有文章未經事先書面授權，請勿任意利用、引用、轉載。